머신러닝에서 데이터 스케일링을 하는 이유는,
SVM과 신경망기법, 그리고 unsupervised learning 등에서 데이터 스케일링이 모델 성능에 영향을 미치는 일이 발생하기 때문이다.
대표적으로 네가지를 언급하겠다.
1. Standard Scaler : 일반적인 데이터 표준화 Z. 평균과 분산을 사용.
2. Robust Scaler : 평균, 분산 대신 중위값과 사분위수를 사용. 평균과 분산과 달리 outlier에 의해 중위값과 사분위수는 거의 영향을 받지 않으므로, oulier의 영향력이 적다.
3. MinMaxScaler : X - min / max−min. 즉 ,변환값이 0과 1사이에 위치
4. normalizer : 변환값이 단위원 위에 위치토록 한다. 즉, 각 데이터 포인트가 다른 비율로 scaling 함. 벡터의 길이는 상관없없고 데이터의 방향만이 중요할 때 사용된다.

scikit-learn을 이용하여 적용해보자.
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(cancer.data, cancer.target, random_state = 1)1. sklearn의 cancer data를 이용하여 훈련세트와 테스트세트를 나누었다.
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
scaler.fit(X_train)
#transform 메서드를 이용하여 X_train data scaling
X_train_scaled = scaler.transform(X_train)2. Scaler을 적합하고 적용하는 것은 여타 머신러닝 기법과 비슷하다.
- 어느 데이터셋 에 대하여 fit 메서드를 활용하여 Scaler을 적합시킨다. 이는 Scaler가 적합되는 데이터셋과 적용되는 데이터 셋이 다를 경우가 있음을 암시하는데,
이 부분에서 개인적으로 의아했다. 단지 데이터의 표준화 자체가 목적이라면 왜 굳이 다른 데이터셋train에 대하여 적합된 scaler을 test set에 적용하는 것일까?
-어쨌거나, train data에 대하여 fit 된 scaler을 어느 data 에 대하여 적용하기 위해서는, transfrom 메서드를 사용한다.
여기서 질문.
scaler = QuantileTransformer(n_quantiles = 50)
X_trans = scaler.fit_transform(X)
plt.scatter(X_trans[:,0], X_trans[:,1], c = y, s = 30, edgecolors = 'black')
왜 train data에 의해 학습된 스케일러를 test set에 적용하는가?
<내 생각>
결국. Scaling의 Target은 모집단이기 때문이다.
train set의 scaling에 사용되는 모수 추정값분산,평균,최대,최소등 은 결국 모집단의 모수의 추정값이다.
만약 test set에 대하여 또 test set 기준으로 scaling을 다시 진행한다면, train, test set을 나눈 의미 자체가 사라져버린다.
두 집단이 동일 기준에 따라 scaling 되지 않았으므로, 표준화 데이터가 왜곡되는 것이다.
추가적으로 sklearn에서 지원하는 scaling 함수들.
1. QuantileTransformer
-각 분위 수에 맞게 데이터를 uniform 분포로 변환.
-정규분포로 출력을 바꾸는 것도 가능하다.
scaler = QuantileTransformer(n_quantiles = 50)
X_trans = scaler.fit_transform(X)
plt.scatter(X_trans[:,0], X_trans[:,1], c = y, s = 30, edgecolors = 'black')
output_distribution 인자를 이용해 분포를 바꿀 수도 있음.
scaler = QuantileTransformer(output_distribution = 'normal', n_quantiles = 50)
X_trans = scaler.fit_transform(X)
plt.scatter(X_trans[:,0], X_trans[:,1])
2. PowerTransformer
회귀분석 시간에 배우지만, power transformation은 정규성이 옅은 데이터들을 정규화시키는데 유용하다.
이 때, power transformation 알고리즘으로 'yeo-johnson' 과 'box-cox'를 선택할 수 있다.
plt.hist(X)
plt.title('Original Data')
plt.show()
X_trans = QuantileTransformer(output_distribution = 'normal', n_quantiles = 50).fit_transform(X)
plt.hist(X_trans)
plt.title('QuantileTransformer')
plt.show()
X_trans = StandardScaler().fit_transform(X)
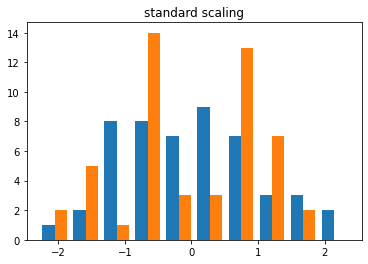
plt.hist(X_trans)
plt.title('standard scaling')
plt.show()
X_trans = PowerTransformer(method = 'yeo-johnson').fit_transform(X)
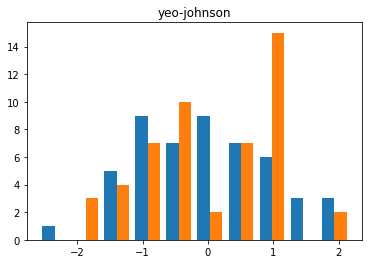
plt.hist(X_trans)
plt.title('yeo-johnson')
plt.show()
X_trans = PowerTransformer(method = 'box-cox').fit_transform(X)
plt.hist(X_trans)
plt.title('box-cox')
plt.show()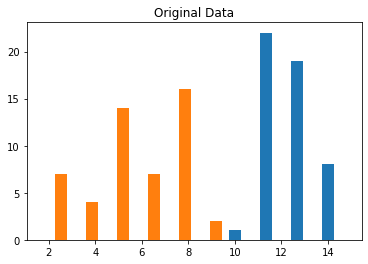
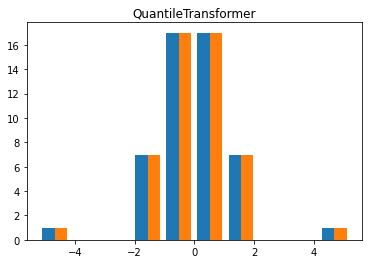
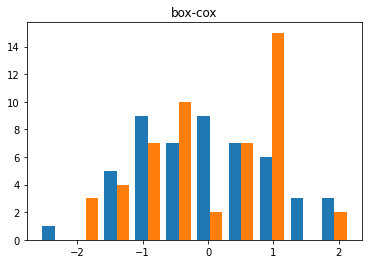
Quantile Transformer과 Powertransformer 에 따른 정규화는 어떤 차이를 지니는가?
Quantile Transformer에 의한 정규화는 백분위수를 기준으로 하므로, 실제 정규분포와 거의 동일하게 분포를 바꾸어 준다. 당연히, 각 데이터에 따라 scaling 정도가 다르게 된다.
반면 powertransformer은, 모든 데이터에 같은 식으로 멱변환을 해준다. 즉, 분석 후에 original y에 대한 값 추론이 가능하다. 이러한 멱변환은 데이터를 정규성을 어느정도 가지게 함이 밝혀졌다.
'ML & AI' 카테고리의 다른 글
| NMF 비음수행렬분해 0 | 2022.07.13 |
|---|---|
| Introduction to Machine Learning with PythonIMLP: Chap 2 지도학습 0 | 2022.07.10 |
| Random Forest vs Extra Trees 0 | 2022.06.30 |
| RandomForest 의 장단점 0 | 2022.06.30 |
| Logistic Regression 에서의 Regularization 0 | 2022.05.16 |