저번 포스팅에서 회귀계수를 구하는 방법 대하여 다뤘다.
회귀계수 추정값을 구하고 나서의 문제는, 이 회귀계수가 실제값이랑 얼마나 차이가 나느냐일 것이다. 왜냐하면 회귀계수를 구하는데 우리가 사용한 데이터는 모집단에서 일부분을 추출한 '표본'이기 때문이다.
그렇다면, 회귀계수를 어떻게 검정할 것인가를 생각해보자.
다행히 이러한 검정을 위해, 통계학자들은 이러한 상황에서 유용하게 쓰일 수 있는 여러 분포를 정립시켜 놓았다.
결론적으로 말하면, 다음 단순회귀모형 Y = Bo + B1x에서 (y, bo, b1은 추정값)
Bo, B1을 표준화한 Zo, Z1의 분포는 표준정규분포를 따른다. 다만, 이 때 Var(Bo)와 Var(B1)을 추정하는 과정에서 Zo, Z1이 t분포를 따르는 식으로 변형이 되게 된다.
간단히 말하면 이렇고, 한번 Bo, B1의 분산을 구해보자.
먼저, Bo, B1을 yi에 대한 선형결합으로 바꾸면, 보다 쉽게 분산을 구할 수 있다.(다시말하지만 Bo, B1은 추정값이다. 즉 Bo_hat, B1_hat인것이다)

이렇게 Bo, B1을 y에 대한 선형결합으로 바꾸면, 훨씬 편해진다.

분산의 성질을 이용하여 구해준다.
이때, Yk와 Yl은 독립임을 보일 수 있다.
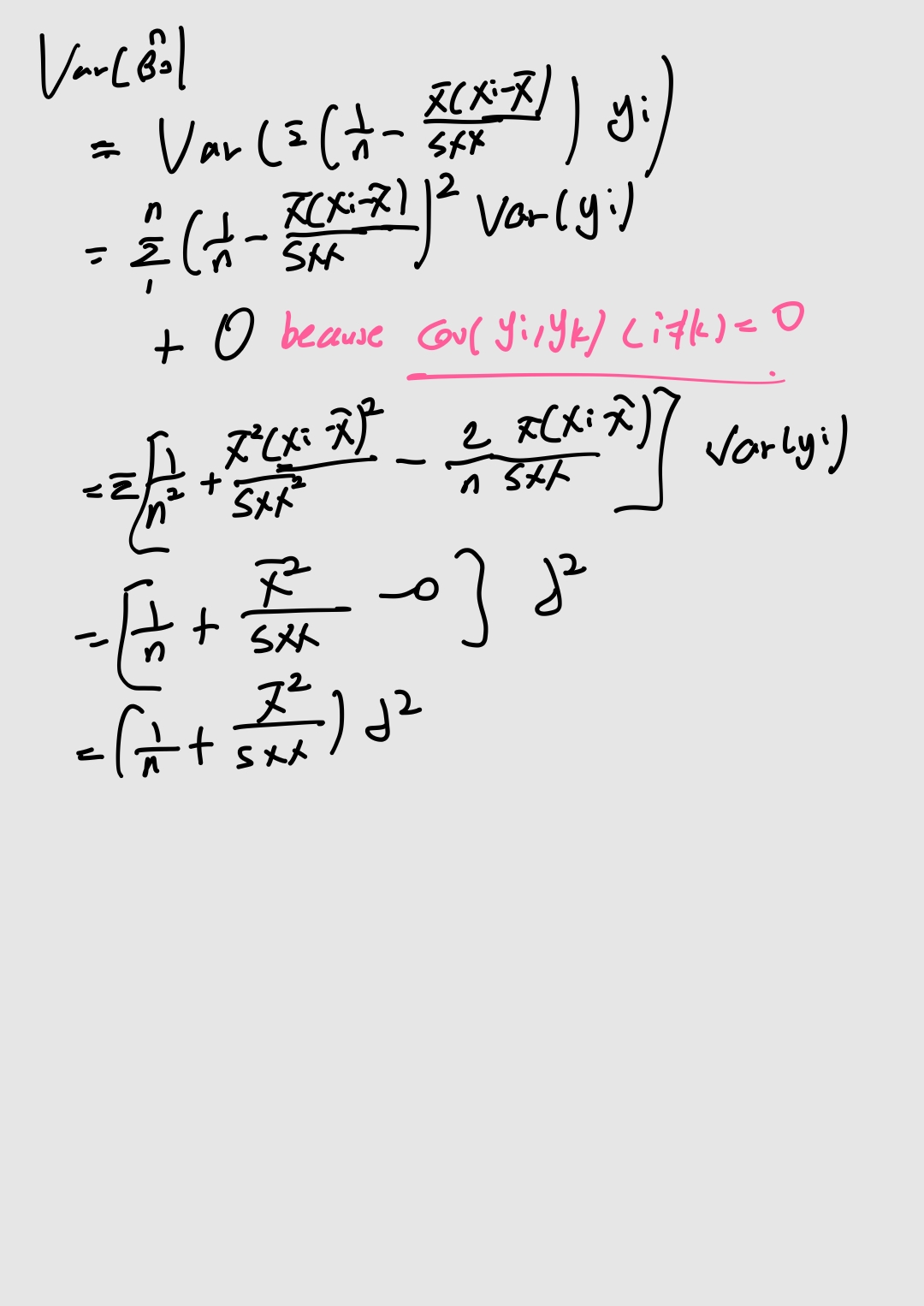
이렇게 구한 분산을 통해 Bo, B1을 표준화하면,
표준화한 (Bo_bar - Bo(참값)) / Var(B0_bar)은 표준정규분포를 따르게 된다.
하지만 우리는 Var(Bo_bar)의 (Var(B1_bar)도 마찬가지) '시그마' 를 미리 알 수 없기 때문에,
시그마^2를 MSE : mean squared error을 이용하여 추정해준다.
이것부턴 다음 글에서..
'Statistic 전공 > 회귀분석' 카테고리의 다른 글
| 모형 타당성 검증 : 잔차분석 (1) | 2022.05.19 |
|---|---|
| <중회귀분석> 2. 중회귀분석 추정계수의 Properties (0) | 2022.05.03 |
| <중회귀분석> 회귀계수 찾기 (0) | 2022.05.03 |
| 1. 단순회귀분석 - 회귀계수의 유도 (0) | 2022.04.27 |

